Gyakorlat 4.
B.Sc course, University of Debrecen, Department of Data Science and Visualization, 2024

class Problem:
"""A formális problémát leíró absztrakt osztálya.
Az __init__, goal_test és path_cost metódusok adott esetben felülírhatók.
A létrehozzott alosztály példányai, megoldhatók a különféle keresési funkciókkal."""
def __init__(self, initial, goal=None):
"""Konstruktor. Szükség esetén további tulajdonságokkal bővíthető"""
# kezdő állapot
self.initial = initial
# cél állapot
self.goal = goal
def actions(self, state):
"""Az adott állapotban végrehajtható műveletek visszaadásár szolgáló metódus.
Az eredmény általában egy lista, de ha sok művelet van, akkor célszerű lehet
iterátor alkalmazás a teljes lista vissza adása helyett."""
raise NotImplementedError
def result(self, state, action):
"""Azt az állapotot adja vissza, amely az adott művelet adott állapotban
történő végrehajtásából adódik.A cselekvésnek a self.actions(state) egyikének kell lennie."""
raise NotImplementedError
def goal_test(self, state):
"""Igaz értékkel tér vissza, ha az adott állapot egy cél állapot.
Az alapértelmezett metódus összehasonlítja az állapotot a self.goal-al,
vagy ellenőrzi a self.goal állapotát, ha az egy lista, a konstruktorban megadottak szerint.
A módszer felülírása szükséges lehet, ha nem elegendő egyetlen self.goal összehasonlítása."""
if isinstance(self.goal, list):
for s in self.goal:
if s==state:
return True
return False
else:
return state == self.goal
def path_cost(self, c, state1, action, state2):
"""Egy olyan megoldási útvonal költségét adja vissza.
Ha a probléma olyan, hogy az elérési út nem számít, ez a függvény csak az állapot2-t nézi.
Ha az elérési út számít, figyelembe veszi a c-t, esetleg az állapot1-et és az akciót.
Az alapértelmezetten a költség 1 az elérési út minden lépéséért."""
return c + 1
def value(self, state):
"""Optimalizálási problémák esetén minden állapotnak van értéke.
A hegymászó és más hasonló algoritmusok megpróbálják maximalizálni ezt az értéket."""
raise NotImplementedError
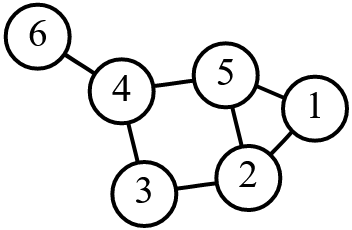
Gráf
class Node:
"""Csomópont a kereső fában.
Tartalmaz egy mutatót a szülőre (a csomópontra, amelynek ez az utódja) és a
csomópont aktuális állapotára.
Egy állapotot két útvonalon érünk el, akkor két azonos állapotú csomópont van.
Tartalmazza azt a műveletet is, amely ebbe az állapotba juttatott minket,
valamint a csomópont eléréséhez szükséges teljes path_cost (más néven g) értéket.
Más függvények hozzáadhatnak egy f és h értéket;
lásd a best_first_graph_search és az astar_search leírását az
f és h értékek kezelésének magyarázatához."""
def __init__(self, state, parent=None, action=None, path_cost=0):
"""Node osztály konstruktora."""
self.state = state
self.parent = parent
self.action = action
self.path_cost = path_cost
self.depth = 0
if parent:
self.depth = parent.depth + 1
def __repr__(self):
"""Speciális metódus mely az objektum string állapotát definiálja"""
return "<Node {}>".format(self.state)
def __lt__(self, node):
"""Speciálist metódus mely definiálja hogy az adott Node objektum
mikor kisebb e egy másik Node objektumnál"""
return self.state < node.state
def __eq__(self, other):
"""Speciálist metódus mely definiálja hogy az adott Node objektum
mikor egyenlő egy másik Node objektummal"""
return isinstance(other, Node) and self.state == other.state
def __hash__(self):
"""Speciális metódus mely definiálja hogy egy adott Node objektum
hash állapotát definiálja"""
return hash(self.state)
def child_node(self, problem, action):
"""A következő csomópont az adott probléma szerinti elkészítése és visszaadása"""
next_state = problem.result(self.state, action)
next_node = Node(state = next_state,
parent = self,
action = action,
path_cost = problem.path_cost(self.path_cost, self.state, action, next_state))
return next_node
def expand(self, problem):
"""A csomópontból egy lépésben eléhető csomópontok visszadása"""
return [self.child_node(problem, action) for action in problem.actions(self.state)]
def solution(self):
"""A gyökér csomópontól a csompontig terjedő műveletek listájának visszaadása"""
return [node.action for node in self.path()[1:]]
def path(self):
"""A gyökér csomópontól a csompontig vezető utvonal csomópontjainak listája"""
node, path_back = self, []
while node:
path_back.append(node)
node = node.parent
return list(reversed(path_back))
Keresők
Próba-hiba

Hegymászó módszer

Problémák
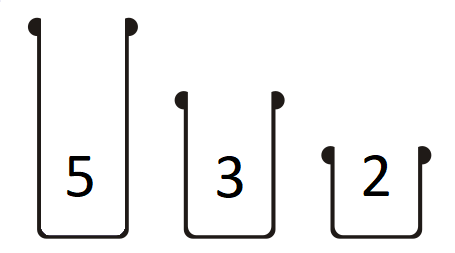
class Cup3(Problem):
def actions(self, state):
"""Operátorok definiálása"""
acts = []
five, three, two = state
if five > 0 and three < 3:
acts.append("5-->3")
if five > 0 and two < 2:
acts.append("5-->2")
if three > 0 and five < 5:
acts.append("3-->5")
if three > 0 and two < 2:
acts.append("3-->2")
if two > 0 and five < 5:
acts.append("2-->5")
if two > 0 and three < 3:
acts.append("2-->3")
return acts
def result(self, state, action):
"""Operátorok hatásának definiálása"""
five, three, two = state
if action == "5-->3":
m = min(five, 3-three)
return (five-m, three+m, two)
if action == "5-->2":
m = min(five, 2-two)
return (five-m, three, two+m)
if action == "3-->5":
m = min(three, 5-five)
return (five+m, three-m, two)
if action == "3-->2":
m = min(three, 2-two)
return (five, three-m, two+m)
if action == "2-->5":
m = min(two, 5-five)
return (five+m, three, two-m)
if action == "2-->3":
m = min(two, 3-three)
return (five, three+m, two-m)
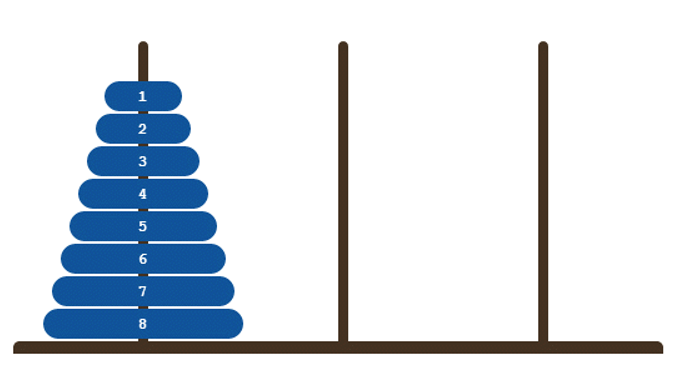
from collections import namedtuple
State=namedtuple("State", ["disk","char"])
class Hanoi(Problem):
def __init__(self, n):
# n darab korongunk van
self.size = n
# "1" * n : Kezdő állapot. Hány darab korng van az 1-es rúdon
# "3" * n : Cél állapot. Hány darab korong van a 2-es rúdon
super().__init__("1" * n, "3" * n)
def actions(self, state):
"""Operátorok definiálása"""
acts = []
# Nézzük meg az egyes rúdak állapotát
f1 = state.find("1")
f2 = state.find("2")
f3 = state.find("3")
# Ha az 1. rúd nem üres és tartalma kisebb mint ami
# a 2. rúdon van vagy a 2. rúd üres akkor
# 1. rúdról átrakhatunk a második rúdra
if -1 < f1 and (f1 < f2 or f2 == -1):
acts.append(State(f1, "2"))
if -1 < f1 and (f1 < f3 or f3 == -1):
acts.append(State(f1, "3"))
if -1 < f2 and (f2 < f1 or f1 == -1):
acts.append(State(f2, "1"))
if -1 < f2 and (f2 < f3 or f3 == -1):
acts.append(State(f2, "3"))
if -1 < f3 and (f3 < f1 or f1 == -1):
acts.append(State(f3, "1"))
if -1 < f3 and (f3 < f2 or f2 == -1):
acts.append(State(f3, "2"))
return acts
def result(self, state, action):
"""Operátorok hatásának definiálása"""
# diks = korong, char = rúd
disk, char = action
# Előtte és utánna lévő korongok helyeinek összefűzése
return state[0:disk] + char + state[disk + 1:]
Nem informált keresési stratégiák
Tulajdonságuk, hogy csak a probléma definiálásakor megadott informárciókat használják fel
Példák nem infromált keresési stratégiákra:
- Szélességi keresés (Breadth first)
- Mélységi keresés (Depth first)
- Egyenletes költségű keresés (Uniform cost)
- Mélységkorlátozott keresés (Depth limited)
- Iteratívan mélyülő mélységi keresés (Iterative depth first)
Szélességi keresés
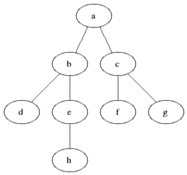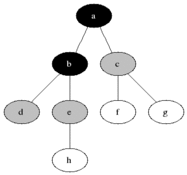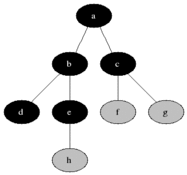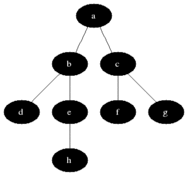
FIFO

# FIFO -> Azt vesszük ki elsőnek amiket beleraktunk
from collections import deque
que = deque([1,2,3,4])
for i in range(2):
print(que.popleft())
print(que)
BFTS
def breadth_first_tree_search(problem):
# kezdő állapot kiolvasása és FIFO sorba helyezése
frontier = deque([Node(problem.initial)])
# Amig nem értük el a határt
while frontier:
# legszélsőbb elem kiemelése
node = frontier.popleft()
# ha cél állapotban vagyunk akkor vége
if problem.goal_test(node.state):
return node
# A kiemelt elemből az összes új állapot legyártása az operátorok segítségével
frontier.extend(node.expand(problem))
print(node.state)
# Hanoi példányosítása
h = Hanoi(3)
print(h.size, h.initial, h.goal)
# Szélességi keresés futtatása
breadth_first_tree_search(h).solution()
# 3 korsó példányosítása
c = Cup3((5,0,0), [(4,1,0),(4,0,1)])
print(c.initial, c.goal)
# Szélességi keresés futtatása
breadth_first_tree_search(c).solution()
Mélységi keresés
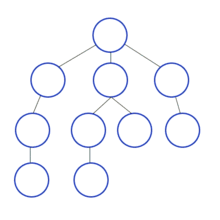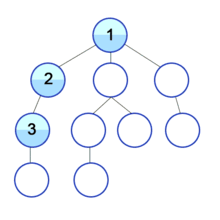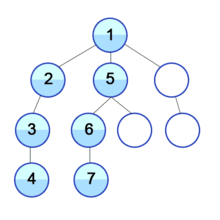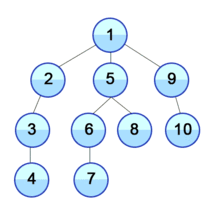
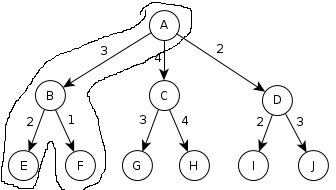
Verem
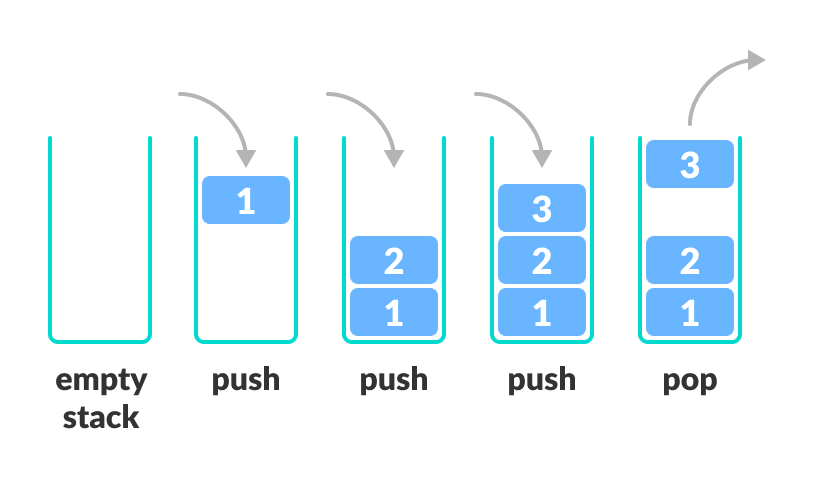
# Verem
stack = [1,2,3,4]
for i in range(2):
print(stack.pop())
stack
Hurok probléma

DFGS
def depth_first_graph_search(problem):
# Kezdő elem verembe helyezése
frontier = [(Node(problem.initial))]
# halmaz deklarálása a már bejárt elemekhez
explored = set()
# Amig tudunk mélyebre menni
while frontier:
# Legfelső elem kiemelése a veremből
node = frontier.pop()
# ha cél állapotban vagyunk vége
if problem.goal_test(node.state):
return node
# állapot feljegyzése hogy tudjuk hogy már jártunk itt
explored.add(node.state)
# verem bővítése amig benemjárt elemekkel
frontier.extend(child for child in node.expand(problem)
if child.state not in explored and child not in frontier)
print(node.state)
# Hanoi példányosítása
h = Hanoi(3)
print(h.size, h.initial, h.goal)
# Szélességi keresés futtatása
depth_first_graph_search(h).solution()
# 3 korsó példányosítása
c = Cup3((5,0,0), [(4,1,0),(4,0,1)])
print(c.initial, c.goal)
# Szélességi keresés futtatása
depth_first_graph_search(c).solution()
