Gyakorlat 5.
B.Sc course, University of Debrecen, Department of Data Science and Visualization, 2024
Ismétlés

# To Do
# Mit csinál a konstruktor?
# Mit csinál a action metódus?
# Mit csinál a result metódus?
# Mit csinál a goal_test metódus?
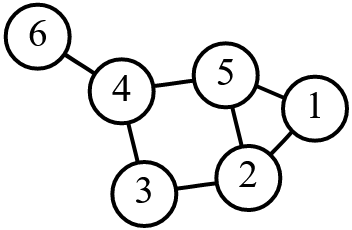
Gráf
# To Do
Keresők
Próba-hiba

# To Do
Hegymászó módszer

# To Do
# Mi az a Heurisztika?
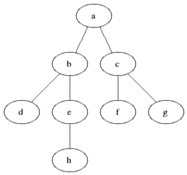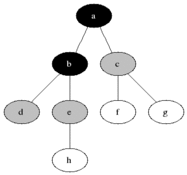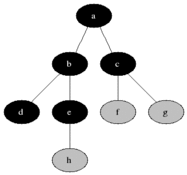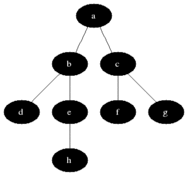
Szélességi keresés
# To Do
# Mi az a FIFO?
Mélységi keresés
# To Do
# Mi az a VEREM?
3 N királynői
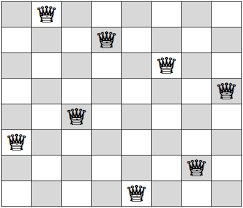
Jellemzők

Állapotok halmaza
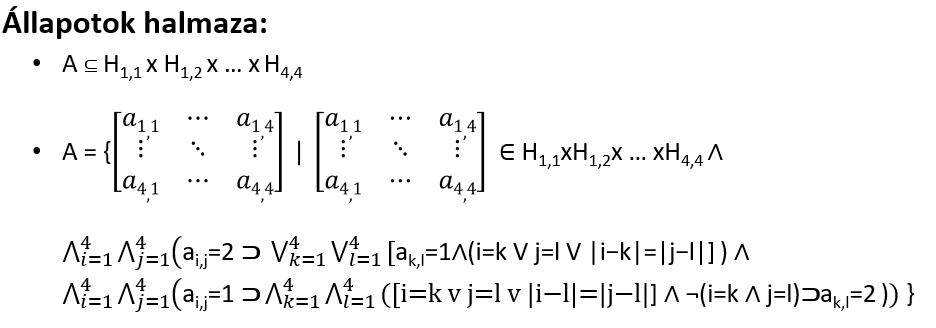
Kezdő állapot
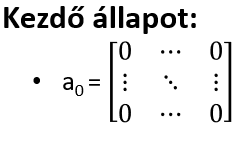
Célállapotok
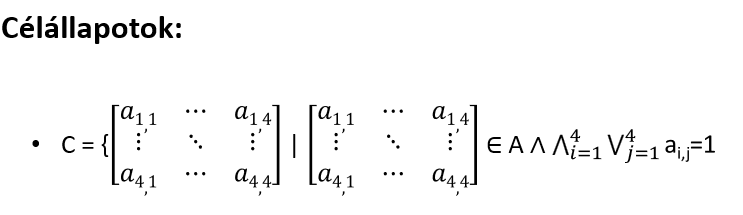
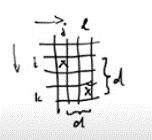
Operátorok
Implementáció
class NQueens(Problem):
"""N királynő elhelyezésének problémája egy NxN táblán úgy, hogy egyik sem üti a másikat.
Egy állapotot N-elemű tömbként ábrázolunk, ahol a c-edik bejegyzésben szereplő r értéke azt jelenti, hogy a
c oszlopban, az r sorban van egy királynő, a -1 érték pedig azt, hogy a c-edik oszlop még nem lett kitöltve.
Balról jobbra töltjük ki az oszlopokat.
"""
def __init__(self, N):
super().__init__(tuple([-1] * N))
self.N = N
def actions(self, state):
"""A bal szélső üres oszlopban próbálja ki az összes nem ütköző sort. """
if state[-1] != -1:
return [] # Minden oszlop kitöltve;
else:
col = state.index(-1)
return [row for row in range(self.N)
if not self.conflicted(state, row, col)]
def result(self, state, row):
"""Helyezze a következő királynőt a megadott sorba."""
col = state.index(-1)
new = list(state[:])
new[col] = row
return tuple(new)
def conflicted(self, state, row, col):
"""Egy királynő elhelyezése (sor, oszlop) ütközik?"""
return any(self.conflict(row, col, state[c], c)
for c in range(col))
def conflict(self, row1, col1, row2, col2):
"""Összeütközésbe kerülne két királynő elhelyezése (sor1, oszlop1) és (sor2, oszlop2)?"""
return (row1 == row2 or # ugyanabban a sorban
col1 == col2 or # ugyanabban az oszlopban
row1 - col1 == row2 - col2 or # ugyanabban az átlóban, irány: \
row1 + col1 == row2 + col2) # ugyanabban az átlóban, irány: /
def goal_test(self, state):
"""Ellenőrizze, hogy minden oszlop megtelt-e és nincs ütközés."""
if state[-1] == -1:
return False
return not any(self.conflicted(state, state[col], col)
for col in range(len(state)))
def h(self, node):
"""Az ütésben lévő királynők számát adja vissza egy adott csomóponthoz"""
num_conflicts = 0
for (r1, c1) in enumerate(node.state):
for (r2, c2) in enumerate(node.state):
if (r1, c1) != (r2, c2):
num_conflicts += self.conflict(r1, c1, r2, c2)
return num_conflicts
nq4 = NQueens(4)
print(nq4.initial, nq4.goal)
nq4 = NQueens(4)
# To Do: próbahiba módszer
nq4 = NQueens(4)
# To Do: szélességi keresés
nq4 = NQueens(4)
# To Do: mélységi keresés
A* algoritmus
def best_first_graph_search(problem, f):
"A best-first kereső olyan keresőfával kereső, mely a legkisebb heurisztikájú nyílt csúcsot választja kiterjesztésre."
# kezdő állapot létrehozása
node = Node(problem.initial)
# prioritásos (valamilyen heurisztika szerint rendezett) sor létrehozása
frontier = []
# kezdő állapot felvétele a prioritásos sorba
frontier.append(node)
# halmaz létrehozása a már megvizsgál elemekhez
explored = set()
# amíg találunk elemet
while frontier:
# elem kivétele a verem tetejéről
node = frontier.pop()
# ha cél állapotban vagyunk akkor kész
if problem.goal_test(node.state):
return node
# feldolgozott elemek bővítése
explored.add(node.state)
# operátorral legyártott gyermek elemek bejárása
for child in node.expand(problem):
# ha még nem dolgoztuk fel
if child.state not in explored and child not in frontier:
frontier.append(child)
# Rendezzük a listát (sort) a heurisztikának megfelelően
frontier = f(frontier)
print(node.state)
def astar_search(problem, f=None):
"""
Az A*-algoritmus olyan A-algoritmusfajta, mely garantálja az optimális megoldás előállítását.
h*(n) : az n -ből valamely célcsúcsba jutás optimális költsége.
g*(n) : a startcsúcsból n -be jutás optimális költsége.
f*(n)=g*(n)+h*(n) : értelemszerűen a startcsúcsból n -en keresztül valamely célcsúcsba jutás optimális költsége."""
return best_first_graph_search(problem, f)
tmp = [Node((3,2,-1,-1)), Node((3,-1,-1,-1)), Node((1,2,-1,0))]
tmp
# Ez nem egy optimális heurisztika!
# Az út költsége legyen 1 és válasszuk mindig a legnagyobb indexű pozivót. Tegyük fel hogy ez az optimális heurisztika
def sort_by_heur(items):
"""Válasszuk mindig a lehető legnagyobb indexű sort"""
return sorted(items, key=lambda x: sum(x.state))
sort_by_heur(tmp)
nq4 = NQueens(4)
print(nq4.initial, nq4.goal)
print(astar_search(nq4, sort_by_heur))
# To Do: 8 király nó probléma a csilaggal.
