Gyakorlat 6.

B.Sc course, University of Debrecen, Department of Data Science and Visualization, 2024

Kényszerkielégítéses feladatok

Általánosan

Mi a különbség egy általános fakeresési valamint egy kényszer-kielégítési probléma között?

Általános keresési probléma
- Az állapot egy fekete doboz
- Az állapotot bármilyen adatstruktúra ábrázolhatja
- Csak az állapotátmenetek, heurisztika és célállapot legyen implementálva
Kényszerkielégítési probléma
- Az állapotot Di tartományból származó Xi változókkal definiáljuk
- A célteszt kényszerek halmaza, mely mindegyike a változók egy részhalmazát és megfelelő értékeket tartalmazzák

Típusai

Változórendezés
- A legkevesebb fennmaradó érték heurisztika (MRV)
- Fokszám heurisztik
Értékrendezés: Legkevésbé–korlátozó–érték heurisztika
Előrenéző ellenőrzés
A kényszerek terjesztése
Élkonzisztencia</br>

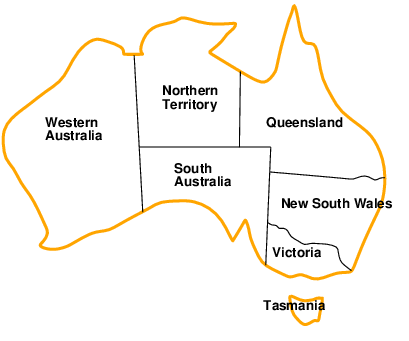
Australia

Milyen adatokkal lehet megadni egy kényszer-kielégítési feladatot?

változók: WA, NT, Q, NSW, V, SA, T
tartományok: Di = {piros, zöld, kék}
kényszerek: szomszédos tartomány nem lehet ugyanolyan színű: WA ≠ NT

Bináris kényszerkielégítési feladat

Minden kényszer maximum két változót tartalmaz
Kényszergráf: a csúcsok a változók, az élek a kényszereket jelölik

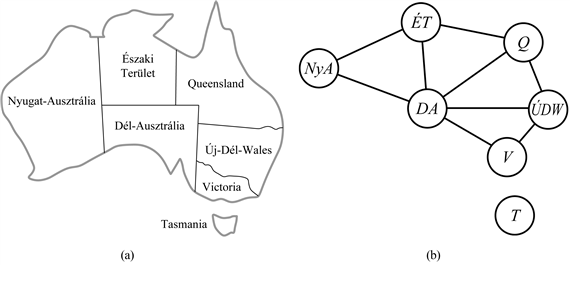
Australia Graf

a gráf szerkezetét felhasználva a keresés felgyorsítható
Tazmánia független részprobléma

Gráf szinezési probléma

A gráf színezési probléma egy olyan probléma, amelyben egy gráfot kell színezni úgy, hogy minden csúcsot egy adott színnel kell jelölni, úgy hogy a szomszédos csúcsok nem lehetnek azonos színűek. A cél az, hogy minél kevesebb színt használjunk a gráf színezéséhez.
Például, ha van egy gráfunk, amelyben négy csúcs van és három színt használunk (piros, zöld és kék), akkor a gráf színezési problémája az lenne, hogy megtaláljuk azt a színezést, amelyben minden csúcsot egy adott színnel jelölünk úgy, hogy a szomszédos csúcsok nem lehetnek azonos színűek.
Ez egy NP-teljes probléma, ami azt jelenti, hogy nincs ismert polinomiális időben futó algoritmus a megoldására. Azonban vannak olyan heurisztikus algoritmusok és approximációs algoritmusok, amelyek közelítő megoldást adnak a problémára.

    # Képezzük le gráfra Ausztráliát
    graph = [[0, 1, 1, 0, 0, 0],
            [1, 0, 1, 1, 0, 0],
            [1, 1, 0, 1, 1, 1],
            [0, 1, 1, 0, 1, 0],
            [0, 0, 1, 1, 0, 1],
            [0, 0, 1, 0, 1, 0]]

    import networkx as nx
    import matplotlib.pyplot as plt

    G = nx.Graph()
    for i in range(len(graph)):
        for j in range(i+1, len(graph)):
            if graph[i][j]:
                G.add_edge(i+1, j+1)

    pos = nx.spring_layout(G)
    nx.draw(G, pos)
    nx.draw_networkx_labels(G, pos)
    plt.show()

Visszalépéses keresés

A kényszerkielégítési feladatra alkalmazott mélységi keresést, ahol egyszerre egy változó kap értéket és visszalép, ha már nincs megengedett hozzárendelési lehetőség visszalépéses keresésnek nevezzük.
A visszalépéses keresés az alapvető nem informált módszere a kényszerkielégítési feladatoknak

    def is_safe(graph, color, v, c):
        """
        A is_safe függvény ellenőrzi, hogy egy adott szín biztonságos-e egy adott csúcson. 
        Ha a csúcsnak van olyan szomszédja, amelynek már ugyanaz a színe van mint a vizsgált színű csúcsnak akkor az nem biztonságos.
        """
        for i in range(len(graph)):
            if graph[v][i] and c == color[i]:
                return False
        return True

    import numpy as np

    def backtracking(graph, graf_colors, v, colors, h=None):
        """A graph_coloring_util függvény rekurzívan meghívja önmagát minden csúcsra és megpróbálja kiválasztani a színeket. 
        Ha egy adott szín nem biztonságos (azaz ha már használják egy szomszédos csúcson), akkor kipróbál egy másik színt. 
        Ha egyik szín sem biztonságos, akkor visszalép és megpróbálja újraszínezni az előző csúcsot."""
        
        # Megvizsgáljuk hogy melyik elemnél vagyzunk
        # ha 'v' == a gráf hosszával akkor készen vagyunk
        if v == len(graph):
            return True
        
        # Próbáljuk végig a szineket
        for c in range(colors):
            # Ha kiszinezhető a 'v' csúcs a 'c' színnel
            if h(graph, graf_colors, v, c):            
                
                # színezzük ki a 'v' csúcsot 'c' színnel
                graf_colors[v] = c

                # szinezzük ki a következő csúcsot
                if backtracking(graph, graf_colors, v + 1, colors, h):
                    return True
                
                # ha nem sikerül visszalépünk és az aktuálisan
                # kiszinezett csúcsot '-1'-re azaz szín nélkülire állítjuk
                graf_colors[v] = -1

    return False

    # Mennyi színnel színezzünk
    colors = 3
    # Legyen -1 a szintelen
    non_color = -1
    # Hozzunk létre egy listát ami tartalmazza az egyes csúcsok színeit
    graf_colors = [non_color] * len(graph)
    print(graf_colors)

    backtracking(graph, graf_colors, 0, colors, is_safe)

    if non_color not in graf_colors:
        print("A gráf színezése: ", graf_colors)
    else:
        print("Nem találtam megoldást a megadott színekkel.")

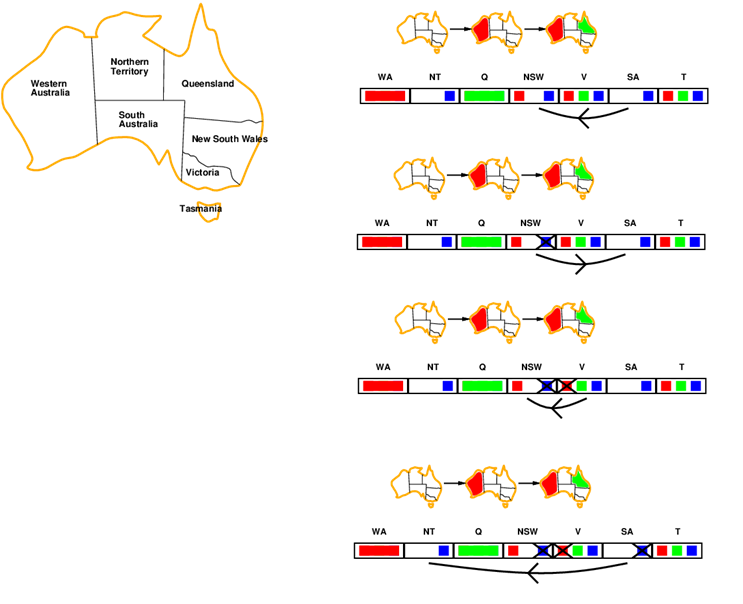
Élkonzisztencia ellenőrzés

Az él a kényszergráf irányított éleit jelenti.
az X -ből Y -ba mutató él akkor konzisztens, ha X minden x értékéhez található egy xszel konzisztens y értéke Y -nak.
- Egy él konzisztenssé tehető az olyan értékek törlésével, amelyhez nem létezik a végpontnak megengedett értéke.
- Az élkonzisztencia ellenőrzés lehetővé teszi, hogy korábban észrevegyük az egyszerű előrenéző ellenőrzés által fel nem fedett inkonzisztenciát.
- Alkalmazható előfeldolgozó lépésként a keresés megkezdése előtt.
- A keresési folyamat minden egyes hozzárendelését követő terjesztési lépésként (az élkonzisztencia fenntartásának algoritmusa).
- Mindkét előző esetben addig kell ismételve alkalmazni a folyamatot, amíg nem marad inkonzisztencia.
- Ugyanis a törléssel a változóhoz mutató éleknél új inkonzisztencia jöhet létre.
- Ha az X változó egy értékét töröljük, akkor X szomszédait újra kell vizsgálni